(시계열) 시계열 모델 기초(3) – 다변량 시계열 ARCH, GARCH 모델

*실무에서 많이 사용하는 모델은 아니지만 개념적으로는 꼭 알아야 할 모델입니다.

변동성 시계열 모델은 기본 가정에서 불안정한 시계열 모델과 다릅니다. 다변량 시계열 모델은 본질적으로 훨씬 더 제한적인 통계 속성에 따라 제한이 있습니다. 따라서 범용성이 낮은 모델이며, 이 모델에 사용할 수 있는 데이터도 제한적임을 알려드립니다. 이는 복잡성이 높은 모델에 해당됩니다.

지금까지 본 모델(ARIMA 이하)의 기본 가정은 정규 분포를 따르고 등분산을 따른다는 것입니다. 그러나 변동성 모델의 기본 가정은 문자 그대로 “변동성이 존재한다”는 것이며 변동성은 시간이 지남에 따라 커지거나 작아질 수 있다는 것입니다.

(이는 금융 시계열 데이터에서 주로 나타나는 패턴으로, 거시경제학자들이 이 데이터를 예측하기 위해 만든 모델이라고 한다.)

따라서 실제 가치가 아닌 이 변동성을 예측함으로써 결국 실제 예측의 오류를 줄일 수 있습니다!

(예측 오차의 분산 감소로 표현)

또한 지금까지의 모델들은 간단히 말해서 종속 변수 자체의 과거 값이었습니다. t-1의 값과 변수의 tp까지의 값을 이용한 예측그랬다면 지금부터 예측하기 위해 변동성에 시그마를 더하는(모든 변동성을 더하는) 발상(금융시장의 경우 시간이 지날수록 변동성이 커지는 것이 일반적이라고 합니다. 시장에 유입되는 정보의 양이 늘어난다고 합니다. 상한선도 높아집니다.) 이러한 가정과 예시를 바탕으로 만든 모델임을 이해하자.)

1. 변동성이란?

그럼 먼저 변동성 모델이 정의하는 변동성 자체에 대해 알아보겠습니다. 여기서 변동성은 단지 표준 편차 또는 분산즉, 분산이 크고 불균일성이 큰 모델에 사용됩니다. 위에서 언급했듯이 금융 시계열 모델은 일반적으로 시간이 지남에 따라 변동성이 증가하는 패턴을 보여줍니다. 그래서, 이 패턴을 보여주는 데이터는 우리가 이전에 이야기했던 것입니다. 일반회귀모형은 오차항의 분산이 일정하다는 회귀모형의 기본가정에 어긋나므로 사용할 수 없다.

예를 들어,

각종 경제지표 발표, 금융위기, 재정위기 등 금융시장의 경우 외부 충격(충격) 데이터가 영향을 받습니다.

연예계의 경우 아이돌의 데뷔, 컴백, 해체, 각종 이슈와 스캔들 외부 충격(충격) 데이터가 영향을 받습니다.

또한 이러한 충격은 일반적으로 일정 기간 동안 영향을 미치기 때문에 시계열의 이분산성 (분산 상수 x)가 발생합니다.

2. ARCH 모델 (자기회귀 조건부 이분산성)

*Autoregressive conditional heteroscedasticity model, 즉 시계열에서 흔히 볼 수 있는 autoregressive 모델, 분산의 분산이 큰 모델 ~ 이름에서 모델의 정의를 유추할 수 있습니다. 이 모델은 에 상당한 영향을 미칠 것으로 생각됩니다.

ARCH 모델의 내부를 수식으로 표현하면 다음과 같이 나온다.

ARCH는 다음 세 가지 공식을 결합하여 만든 공식을 사용합니다.

1. 평균 모델(평균 방정식 사용): y_t는 시점 t에서의 시계열 데이터 값입니다. 마지막에ε_t는 오차항으로서 변동성을 의미하며, 이 모델에서는 상수가 아닌 변수요점은 (값 변경 -> 모델이 더 강하게 예측)으로 취급된다는 것입니다.

2. 변동성 모델(분산 방정식 사용): 최종 분산 방정식은 시간 0에서 시간 t-1, 시간 tq까지 변동성의 합입니다. (분산식 앞에 곱셈으로 더한 알파가 가중치)

3. 잔차 모델(ε_t = a_t√h_t 공식): 평균 모델과 변동성 모델에서 예측한 값을 기준으로 남은 오차를 나타냅니다. 여기서 h_t는 조건부 분산입니다.

이러한 방정식을 결합하여 아치 모델은 다양한 유형의 모델을 만들 수 있습니다. 이 수식이 의미하는 바는 시계열 데이터의 평균, 분산, 오차항을 모형화하여 예측하는 것으로, 세 가지 모형을 조합하여 모형을 만들었다는 것이 이해하기 쉬울 것 같습니다.

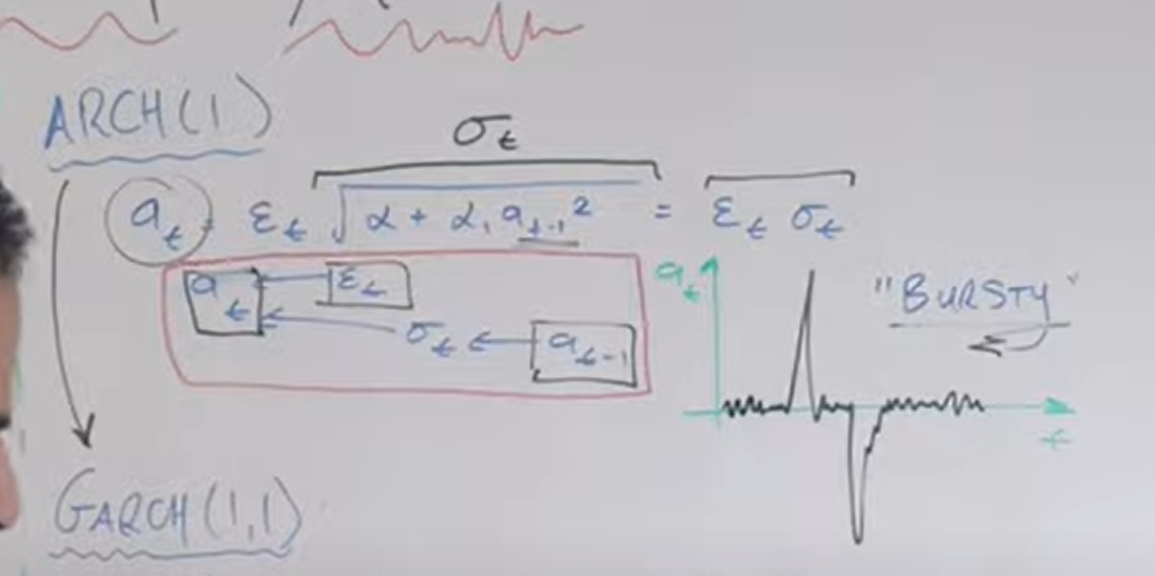
따라서 ARCH 모델은 다음과 같은 단점이 있다. 시계열 데이터 중 금융 데이터의 변동성을 예측한 모델이지만…

1. 양의 변동성과 음의 변동성(충격)은 동일합니다.(변동성의 방향이 양(+) 또는 음(-)인 경우를 고려하여 가격 하락과 상승을 유사하게 취급함을 의미)

2. 기본적으로 정상성을 가정한 모델 (길이가 짧아도 비정상적인 시계열 데이터에는 사용할 수 없음)

삼. 매개 변수를 결정하기 어려움. 그 이유는 모델이 복잡하기 때문입니다.

이러한 이유로 ARCH를 개량한 GARCH 모델을 주로 사용한다. GARCH 역시 시계열 데이터에서 변동성이 일정하지 않다고 가정한 모델이지만, 변동성의 시계열 의존성, 즉 자기상관을 표현하는데 있어 매개변수의 수를 줄일 수 있는 장점이 있다.

---

3. GARCH 모델(일반화된 자기회귀 조건부 이분산성)

GARCH 모델은 ARCH 모델과 마찬가지로 변동성이 어떻게 변하는지 예측하는 모델입니다. 이 모델은 변동성을 설명하는 가중치, 알파 및 베타를 사용하여 조건부 분산을 계산합니다. GARCH 모델은 변동성이 양의 변동성과 음의 변동성을 동등하게 취급한다는 점에서 ARCH 모델과 다릅니다. (앞서 언급한 ARCH의 이 한도 계산)

수식을 자세히 보면 ARCH와 다릅니다. 시그마 t(변동성) 부분을 계산하는 루트의 또 다른 변동성 요인이 영향을 받은 것으로 간주됩니다. 따라서 나의 현재 가치를 예측하기 위해 사용된 이전 가치의 변동성은 이전 가치의 두 가지 변동성에 영향을 받는 것을 알 수 있다. 따라서 예측된 시계열 값을 그래프로 나타내면 버스트(폭발적인 상승 또는 하강)가 적게 나타납니다. 이전 기간의 변동성을 더 강한 수준으로 간주하기 때문입니다. (시간이 더 걸리기 때문에)

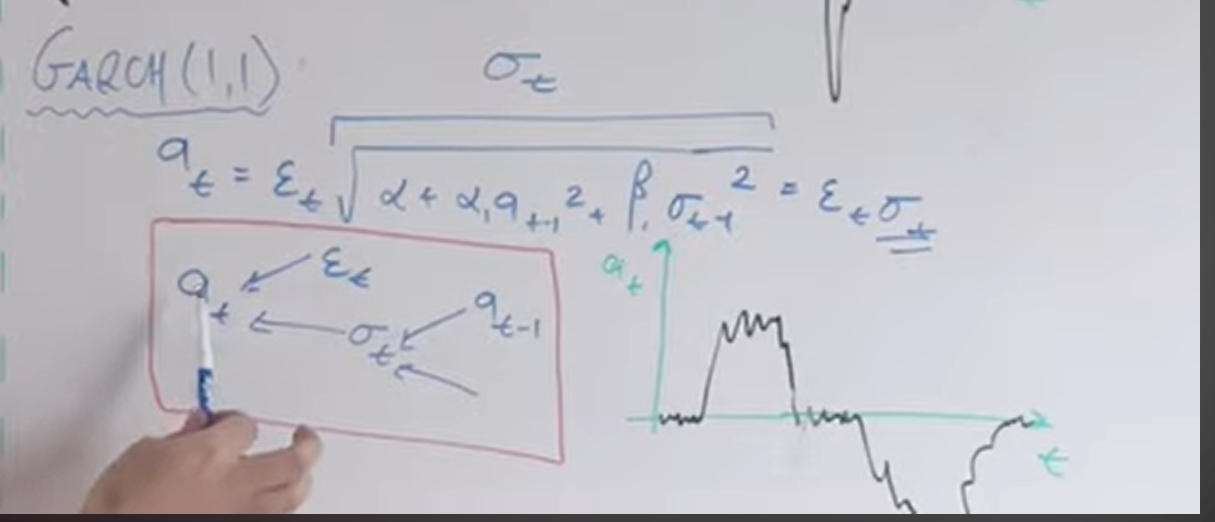
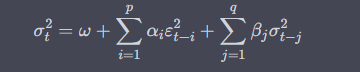
GARCH 모델을 이해하기 위해 인강이 하는 말을 정말 몰라서 이 선생님의 도움을 받았는데…

(참조)

https://www.youtube.com/watch?v=inoBpq1UEn4

파이썬을 연습할 수는 있지만 어차피 실전에서는 사용하지 않기 때문에 이 포스팅에서는 생략한다.

(참조)